
2014-11-26 22:19 来源:818期货学习网
Black-Scholes模型
随机波动率实质上就是跳出了传统金融市场以一定时期内波动率作为恒定参数考虑市场的框架,而认为波动率本身是随着价格变化而变化的,这一变化过程符合随机过程。在当前的金融市场,因为该类模型考虑的因素更多、理论基础更为严谨而受到不少投资者的关注。
虽然Black-Scholes模型通过随机波动率对期权定价(某些宽松的假设实质上在交易过程中也是可以被接受的),也将影响期权权力的波动率及分布概率等问题引入到整个评估体系中,但当时还有诸多尚未解决的问题,其中一个重要的不足之处在于它对于基础资产价格回报恒定波动率(以及其波动率不受价格变化影响)的假设。这种假设意味着使用期权的对冲者要不断地对波动率假设进行调整来反映实际的市场价格数据,从而导致了对冲比例的不断变化,也导致了传统期权定价模型无法对隐含波动率的一些固有特性给予合理的解释。在现实市场中,Black-Scholes模型给出的期权理论定价也比较难吻合观察到的期权市场价格。
Black-Scholes模型根据当前标的价格和静态波动率来得到当前的期权价格,存在着一些难以克服的缺陷,比如说假设股票价格的收益率是遵循一个固定的均值和方差的正态分布等。但是在实证中我们发现波动率事实上随时间变化有一个集聚过程,这与Black-Scholes模型假设有极大的出入。另外金融界与学术界也意识到金融价格时间序列的分布形态明显体现出尖峰厚尾的回报特点,也即是说市场的尾部风险较高,这实质上是期权定价中一个明显的溢价因素,且不能被固定波动率的假设所捕捉。除此之外,金融价格时间序列中波动率偏离后均值复归的特点也是Black-Scholes模型无法刻画的难点。在期权市场的实际交易中隐含波动率往往呈现波动率微笑形态,随着执行价格不同位置的变化,期权反推的隐含波动率并不一致。
就波动率本身而言,我们可以由市场数据观察到它的主要特性包括:波动率簇集(volatility clustering)、回报分布尖峰厚尾(high peak/fat tails)导致的高波动率变化以及波动率均值回归(volatility mean-reverting)。其中尖峰厚尾特性是由于有不同方差的分布混合而产生的。显然,要对期权进行准确的定价,对于波动率随机过程的刻画就尤为重要,特别是在非平值期权的定价方面。
出于以上的考虑,我们认为将随机波动率引入到期权定价当中十分有必要。
随机波动率的主要思路是将标的资产价格的波动率描述为一个由价格水平、波动率均值回归趋势和波动率方差控制的随机过程。这样一来就提供了对波动率动态变化进行刻画的方式,进而也提供了对期权进行更加准确定价的可能。
B
Heston模型:刻画波动率变化的基础模型
在克服之前所提到的诸多问题方面,目前业界主流的方法是对传统Black-Scholes模型的一些拓展,比如说我们知道在已知执行价格、标的价格、到期日的情况下,影响期权价格的主要因素是波动率和利率变化,所以可以用随机波动率模型和随机利率模型刻画这两个重要的因子,同时,在考虑波动率分布方面,除了之前提到的诸多特点外,因为它还有跳跃的情况,我们还可以加入随机波动率跳跃模型。如此一来,期权的定价实质上转变为了我们在资产价格、利率水平和风险价格之间平衡的解决方法。为了更加准确地在该框架下以刻画波动率的思路为期权定价,我们使用随机波动率模型来优化期权价格的计算。其中一个比较基础的模型就是Heston模型。
Heston在1993年提出这种模型,并且提供了期权价格的闭式解。由于可以考虑资产价格和资产波动率的相关性,而且假设资产价格有一个扩散的过程,因此在这个模型中,期权的价格是通过计算看涨期权交割在实值区域的概率得到的。下面简单介绍一下其逻辑过程:
Heston模型假设股票价格S服从扩散分布(几何布朗运动),其中以μ这个漂移参数作为波动方向的调整。Heston和B-S最大的区别是在判定波动率时不再认为其是一个常数,而是也服从一个扩散过程。在实际操作过程中可以运用伊藤定理来获得波动率,根据Cox、Ingersoll、Ross三人写出的随机偏微分方程,以不同参数分别刻画波动率均值复归的速度、波动率长期均值及波动率的波动率。此处模型考虑了加入波动率与回报之间相关性的联系,以使得波动率影响得以体现,这有赖两个方程的相关性分析。
相关性参数的刻画尤为重要,因为它反映了价格变动的偏度,也很大程度上显示了价格回报尖峰厚尾的特点。当相关性ρ>0时,会导致厚尾右偏:因为当波动率随回报的变大而变大,会对价格变动起到放大作用。与之相对的,当相关性ρ<0时,会导致价格回报厚尾左偏:因为当波动率随回报的变大而变小,会对价格变动起到减小作用。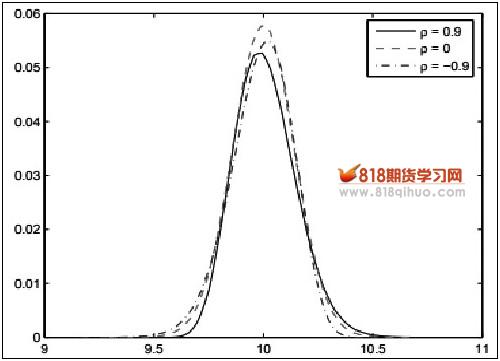
相关性之所以重要,除了上面讨论的一些原因,最重要的还是因为波动率变化的精确捕捉,我们可以在不同相关关系背景下为期权找到正确的价格。在金融市场,特别是股票市场,我们可以观察到明显的杠杆效用(leverage)和崩盘恐惧/巨灾(crash-ophobia)效应。杠杆作用通常被理解为当股票价值下跌会提升公司的财务杠杆比率,这意味着公司股权资产的风险加大,波动率加剧(回报与波动率正相关);而股票价值上升会降低公司的财务杠杆比率,从而降低公司股权资产风险,波动率降低(回报与波动率负相关)。我们知道Black-Scholes模型最大的问题之一就是恒定波动率假设不能捕捉的市场信息过多,也就造成了定价的相应偏差,但是若我们使用Heston模型的假设之后,在不同相关性下自然可以刻画之前期权偏差部分的变化。
© Copyright 2014 818期货学习网 All Rights Reserved. 浙ICP备14000419号-1